公式1:1つが原点である場合 3つの頂点のうち、1つが原点なら、公式はシンプルな形になります。 実際、座標平面上の3点 ( x 1, y 1), ( x 2, y 2), ( 0, 0) を頂点とする三角形の面積は、 1 2 x 1 y 2 − x 2 y 1 となります。 (この公式の証明はページの最後で説明します) 例えば、座標平面上の3点 ( 1, 2), ( 3, 4), ( 0, 0) を頂点とする三角形の面積は、 1 2 1 × 4 − 3 × 2 = 1 「円錐の側面積と中心角が超楽に求められる公式をまとめました! 字が汚くてすみませんm(_ _)m」, 学年 中学全学年, キーワード 数学,空間図形,円錐,中心角,側面積,簡単,math,空間のベクトル,空間ベクトルと空間図形 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための語呂は、
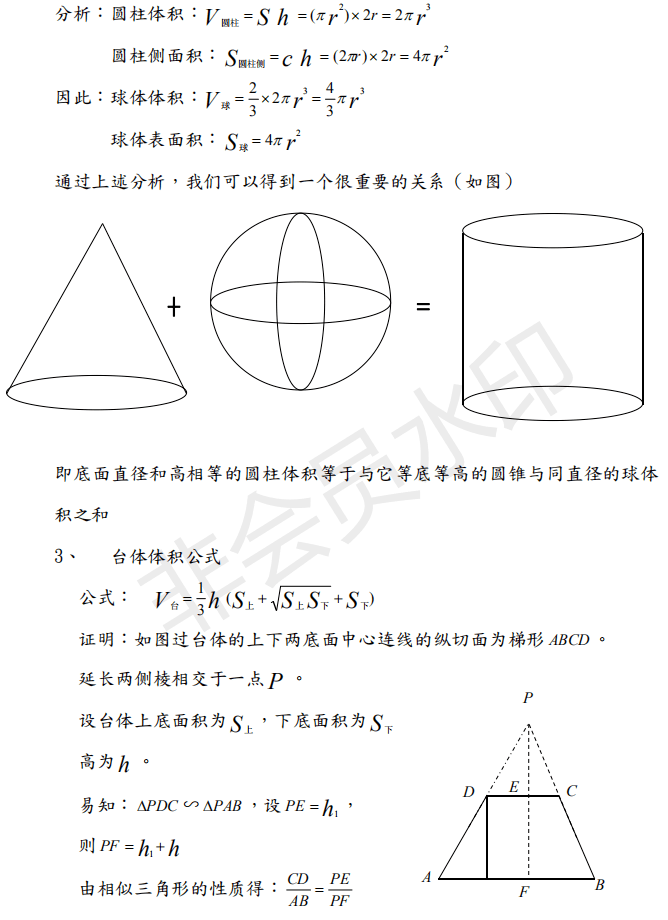
22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理
